Consider
a long pipe of uniform cross section A, and having rigid walls. Fluid is
confined to the interior of a long pipe.
So
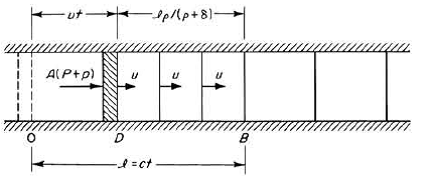
at one end is a piston of negligible mass, which constrains the fluid to stay
to its right. The piston was at rest at point 0 held by the force F=AP
counteracting the equilibrium pressure P of the fluid. Suppose that at time
t=0, the piston is started into motion to the right with constant velocity u.
This action will push the piston to the right increasing the pressure to P+p.
If we want to get a piston into motion we need to increase the force from AP to
A(P+p), where p is related to the change in density of the fluid by the
equation δ=κρp where coefficient of compressibility can be isothermal or
adiabatic.
Originally
δ is related to the change in volume of the compressed fluid, and this is
related to the amount of fluid which has been set in motion at any specified
time t. Since fluid has it’s compressibility and inertia it takes time to get
it into motion. So when the piston is moved from equilibrium position the
starting wave front will travel away from the piston reaching the point B at
time t. Let’s say that in time t the wave has traveled the distance ct where c
is the velocity of the wave. Then all the fluid to the right of this front, at
B is in its original equilibrium condition at rest with density ρ. The fluid in
the region D to B in motion with velocity u of the piston compressed to a
density and thus occupies a volume ρ/( ρ +δ) times its original volume Al=Act.
The difference between this volume and the original volume Act is of course the
volume Aut, swept out by the piston in time t so that
$$\begin{align}
& Aut=Act-\frac{A\rho ct}{\rho +\delta } \\
& \frac{u}{c}=1-\frac{\rho }{\rho +\delta }=\frac{\rho +\delta -\rho }{\rho +\delta }=\frac{\delta }{\rho } \\
\end{align}$$
Where
the last formula is valid only as long as the density change δ caused by the
motion is small compared with the equilibrium density. In traveling the distance ut the piston has done
an amount of work A(P+p)ut which must have gone into additional energy of the
fluid. Part of this energy will be kinetic energy one-half of the mass of the
fluid in motion, 0.5*Aρct times the square of its velocity u². The other part
is potential energy of compression the work done in compressing the fluid from
volume Act to volume Act[ρ/(ρ+δ)]. The work is the integral of the pressure P+p
times the change in volume dV, integrated between these limits. Thus the
potential energy is:
$$\int{\left( P+p \right)V\kappa dp=PV}\kappa p+\frac{1}{2}V\kappa {{p}^{2}}\simeq Aut\left( P+\frac{u}{2\kappa c} \right)$$
Thus
the equation for energy balance becomes:
Force x distance = potential + kinetic energy
The
first terms on both sides cancel. In fact, the work APut should not be charged
to energy of the sound wave, since it is the work done pushing against the
equilibrium pressure; if there had been fluid pressure P on the lef hand
surface of the piston, it would have provided the AP part of the force and only
force Ap would have been required to move the piston.
Potential energy density = 0.5*κp²
Kinetic energy density = 0.5*ρ*u²
For
the energies per unit volume of the sound, correct ot the second order in the
small quantities p and u.
What
we have shown by this manipulation is that the mass of the fluid, represented
by the equilibrium density ρ, and its elasticity, represented by κ, so combine
that it takes time for the motion of one part of the fluid to be transmitted to
another part, the speed of transmission being equal to c=Sqrt(1/ρκ) as long as
the fluid motion is small enough so that the excess pressure p is small
compared with the equilibrium pressure P. The impulse-momentum relationship could
also be used to compute c. The excess force Ap contributes an impulse Apt to
the fluid in time t, which must equal the momentum contributed to the fluid
newly set into motion in time t. The acoustic momentum density of the fluid is
up, so that
$$Apt=\left( u\rho \right)\left( Act \right)\simeq A{{c}^{2}}\delta t$$
It
is obvious that the wave velocity c will be independent of the amplitude and
shape of the sound wave only as long as the sound pressure p is small compared
with the equilibrium pressure P.
For
fluids like water, where K is small enough so that δ/ρ is small even though piP
is not small, another limitation enters. For example, if the piston were pushed
to the left, a wave of rarefaction would be sent along the tube, and if u were
large enough, the p computed from the formulas might be equal to or larger than
P; the piston would be withdrawn rapidly enough to produce a vacuum behind it.
When this happens the fluid loses contact with the piston, leaving a large
bubble of vapor in the interspace, and it is obvious that our equations no
longer hold. Long before this happens the value of K begins to change, so that
K cannot be considered independent of
p
unless Abs[p] is small compared with P.
Nema komentara:
Objavi komentar